La gâche du professeur Tee
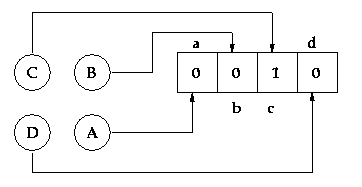
Suite à la disparition de quelques barrettes mémoires dans les salles de travaux pratiques d'informatique, le service travaux-entretien-sécurité de l'université d'Euphoria a décidé d'équiper les portes de serrures à codes. Le budget est limité et les compétences locales ont été réquisitionnées par l'incubateur de l'université pour fabriquer un système original.

[1]
Le registre peut prendre 16 valeurs et sans rien de plus, vous
pourriez ouvrir la porte en moins de huit tentatives. Quelle est la plus
courte série de touches à composer pour ouvrir la porte ?
L'éminent
professeur Tee a sécurisé le système. Chaque fois
que la touche X est pressée un nombre aléatoire de rotations
circulaires est appliquée au registre secret qui passe de l'état
abcdà
l'état bcda
après
chaque rotation. Un cryptogramme du registre s'affiche en permanence sur
un petit écran à cristaux liquides, il dépend
du temps qu'il fait et de la date du jour, seuls les enseignants peuvent
utiliser cette information pour ouvrir la porte.
[2] Comment faites-vous pour ouvrir la porte !
Solutions
 Première
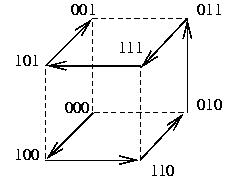
question. Il existe plusieurs solutions, par exemple : XAXBXAXCXAXBXAX.
En effet, il suffit de changer l'état des trois premiers bits du
registre. La façon la plus économique est représentée
par la figure ci-contre. On change successivement les bits :
a, b, a, c, a, b, a. La listes des 3-uplets
qui s'en déduit forme un code de Gray en dimension trois.
Première
question. Il existe plusieurs solutions, par exemple : XAXBXAXCXAXBXAX.
En effet, il suffit de changer l'état des trois premiers bits du
registre. La façon la plus économique est représentée
par la figure ci-contre. On change successivement les bits :
a, b, a, c, a, b, a. La listes des 3-uplets
qui s'en déduit forme un code de Gray en dimension trois.
Plus
généralement un code de Gray de dimension
n est une énumération des
2^n
mots binaires de longueur n
dans laquelle deux éléments consécutifs diffèrent
par un seul bit. Le lecteur pourra illustrer
l'article
de Zimmerman (login du mois d'avril) par l'écriture d'une procédure
Gray(n)
qui imprime un code de Gray sur n bits.
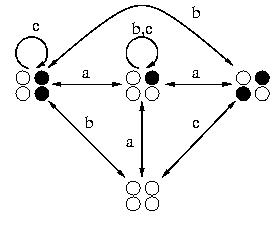
Deuxième question. Il suffit de composer la série XAXACXABXACXACXABXACX.
A priori, le registre secret peut prendre 16 valeurs différentes mais les rotations circulaires font que nous ne devons distinguer que 4 états : quatre bits identiques (xxxx), un bit distingué (xxxy), deux bits consécutifs identiques (xxyy) ou bien aucun bits consécutifs égaux (xyxy). Vis à vis de ces 4 situations, presser une touche ou trois produit le même effet, c'est ce que nous noterons l'action a. Nous considérerons deux autres actions. L'action b qui consiste à presser les touches A et B simultanément et l'action c qui consiste à presser A et C simultanément. Toutes les transitions possibles sont décrites par le diagramme sagittal de la figure ci-contre, c'est le diagramme de transition d'un automate fini non déterministe.
 Nous
allons vérifier qu'il est possible d'ouvrir la porte en 8 tentatives.
En effet, on commence par essayer X, si la porte s'ouvre c'est gagné
sinon nous sommes dans un des trois états de fermetures. Supposons
que le registre soit dans l'état (xxxy). On
commence par presser la touche A puis la touche X, c'est l'action a.
Si la porte s'ouvre c'est gagné sinon nous en déduisons être
dans l'état (xxyy) ou (xyxy). On continue par l'action c,
si la porte s'ouvre c'est gagné sinon nous en déduisons être
dans l'état
(xxyy) et nous continuons par b. Si la porte s'ouvre c'est gagné
sinon nous en déduisons être dans l'état (xyxy), nous
refaisons c. Si la porte s'ouvre c'est gagné sinon c'est
que notre hypothèse initiale était fausse : au départ
nous étions dans l'état (xxyy) ou (xyxy). Mais après
cette série d'actions, nous sommes sûrs d'être dans
l'état (xxxy) et il suffit de recommencer la séquence
cbc.
Nous
allons vérifier qu'il est possible d'ouvrir la porte en 8 tentatives.
En effet, on commence par essayer X, si la porte s'ouvre c'est gagné
sinon nous sommes dans un des trois états de fermetures. Supposons
que le registre soit dans l'état (xxxy). On
commence par presser la touche A puis la touche X, c'est l'action a.
Si la porte s'ouvre c'est gagné sinon nous en déduisons être
dans l'état (xxyy) ou (xyxy). On continue par l'action c,
si la porte s'ouvre c'est gagné sinon nous en déduisons être
dans l'état
(xxyy) et nous continuons par b. Si la porte s'ouvre c'est gagné
sinon nous en déduisons être dans l'état (xyxy), nous
refaisons c. Si la porte s'ouvre c'est gagné sinon c'est
que notre hypothèse initiale était fausse : au départ
nous étions dans l'état (xxyy) ou (xyxy). Mais après
cette série d'actions, nous sommes sûrs d'être dans
l'état (xxxy) et il suffit de recommencer la séquence
cbc.
La
théorie des automates décrit une procédure de déterminisation
qui montrerait que la solution proposée est optimale.