Best Pair of Binary Sequences
This page reports on the best pair of binary sequences
for the auto and cross correlation point of views.
Philippe Langevin,
Last modification February 28th 2014.
Correlation
Let n be a positive integer, f end g two
binary sequences of length n i.e. two mapping
from the cyclic group Z/nZ into {-1,+1}.
The cross correlation between f and g at t
is defined by
fxg (t) = sum_{ y - x = t } f(x) g(y)
in other words, the scalar product between the
vector f and the t-shift of g. One defines the
correlation values :
R(f) = max { f x f (t) | 0 <> t in Z/LZ }
and
I(f,g) = max { f x g (t) | t in Z/LZ }
Terminology
To a given sequence f we associate a polynomial
of degree less than n in a natural way
f(T) = sum_{k} f(k) T^k
We have two products :
f(T) f( 1/T ) = sum_{k} A_k(f) T^k
and
f(T) f( 1/T ) = sum_{k} C_k(f) T^k modulo (T^n - 1)
The coefficients C_k(f) are nothing but the autocorrelation
values of f, the A_k(f) are called aperiodic correlation values.
A sequence with A_k(f) smaller than one in absolute (for k>0)
is called a Barker sequence. Such sequences could be useful
for radar applications but one conjectures the non existence
of Barker sequences of length greater than 13.
A sequence with C_k(f) equals to zero for all k>0 is called
perfect, one conjectures the non existence of such combinatorial
object for n>4.
It is easy to see that
C_k(f) = n modulo 4
a reason why one says a binary sequence has optimal
correlation when
sup_{k>0} | fxf( k)| = 4, 3, 2, 1
according to the congruence of n modulo
4 is : 0, 1, 2, 3.
Objective
Provides datas about the best pair of binary sequences
i.e. pair (f,g) of optimal sequences minimizing
the correlation parameters :
theta( n ) := min sup { f x g (t) | t in ZnZ}
where both f and g are optimal sequences.
Methode
One can see the correlation values of a sequence do not depend
on shift and change of sign.
For the small values of n ( less than 40 ), one can use
a naive approach to compute the distribution of optimal
sequences, here are the codes we used :
[src/countps.c]
[src/genopt.c]
[src/bpbs.c]
[cpu.txt]
The running time for n=41 was about 14 hours,
using 18 cores of the above architecture below,
the same when offloading on xeon phi.
[langevin@mejean COUNTPS]$ cat job.585.out
[Offload] [MIC 0] [File] countps.c
[Offload] [MIC 0] [Line] 99
[Offload] [MIC 0] [Tag] Tag 0
[Offload] [HOST] [Tag 0] [CPU Time] 51451.540086(seconds)
[Offload] [MIC 0] [Tag 0] [CPU->MIC Data] 28 (bytes)
[Offload] [MIC 0] [Tag 0] [MIC Time] 51210.619694(seconds)
[Offload] [MIC 0] [Tag 0] [MIC->CPU Data] 28 (bytes)
L=41 (1) alpha=3 opt=4842
[langevin@mejean COUNTPS]$ cat job.586.out
L=41 (1) alpha=3 opt=4842
[langevin@mejean COUNTPS]$ cat job.586.err
time=14:12:57
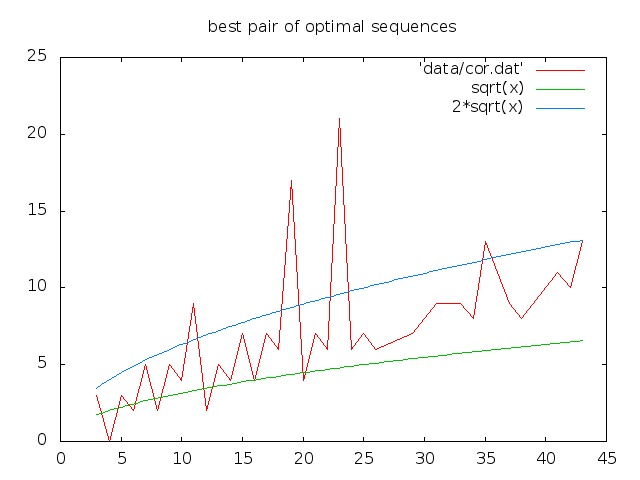
Results
The distribution
of optimal sequences up to shift, up to
change of sign with length less or equal to 43.
The best pairs of optimal sequences are in the
opt-file and bp-file. The
correlation picture :
References
[1] The Cross-Correlation of Binary Sequences With Optimal Autocorrelation,
Cunsheng Ding and Xiaohu Tang,
ieee transactions on information theory, vol. 56, no. 4, april 2010.

