Binomial Weil Sums
This page reports the numerical experiments (Summer 2016)
on Weil sums.
Definitions and notations
Let m be a positive integer, X a nontrivial additive character
of GF(2,m). We consider the Weil sum
W(s,a) := sum_{x in GF(2,m)} X( x^s + ax ).
one defines the valuation of s
val(s) := min_{a!=0} dyadic valuation of W(s,a)
and spectral amplitude of s by
spec(s) := max_{a} absolute value of W(s,a)
The goal of the project is to compute the distribution of
valuations and spectral amplitudes when s ranges among
the invertible exponents, for m smaller or equal to 32.
picture
In the picture below, we plot the graphs
of the quantities :
m -> log_q max_s spec(s)
m -> log_q max_s abs( walsh(s, 1) )
m -> log_q max_s val(s)
where q:=2^m
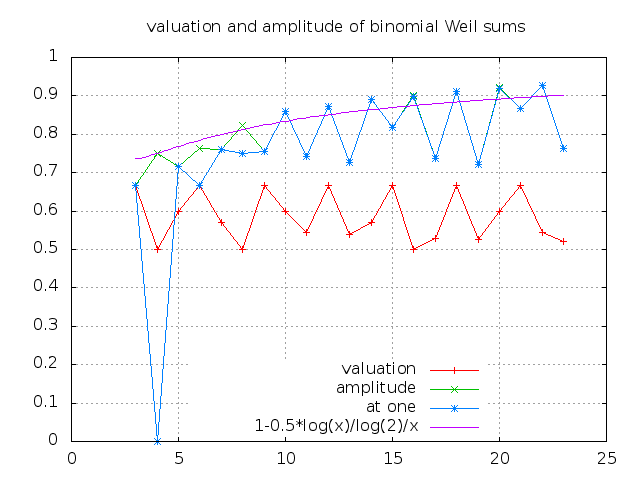
Interpretation
Actually, we have fully understood the non-archimedian profile.
It seems enough to understand the Fourier
coefficient at one.
Computation
Methodology
Philippe Langevin, Summer 2016

