let
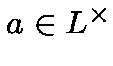
let
Letbe an extension of degree
of
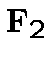
let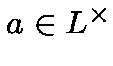
letbe an integer, and consider the boolean function
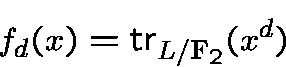
If
is odd the
If
is even
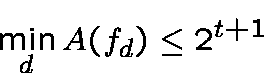
The Fourier tansform ofis given by
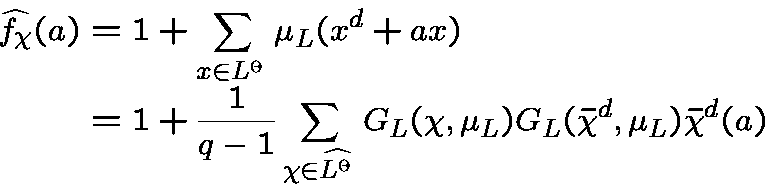
where 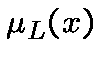 is the canonical additive character of
is the canonical additive character of ![]() .
Note that by Fourier inversion :
.
Note that by Fourier inversion :
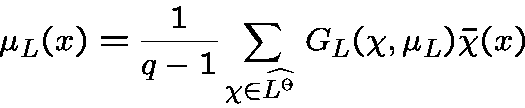
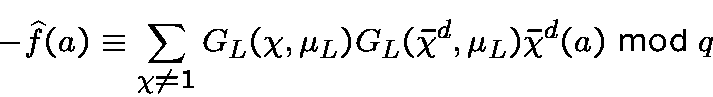
We isolate the parameters
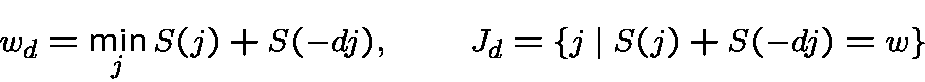
![\begin{displaymath}\widehat{f_\chi}(a) = 2^w\big[\sum_{j\in J_d} \bar\omega^{jn}(a)\big] \pmod{2^{w_d}\wp}\end{displaymath}](img247.gif)
For all,
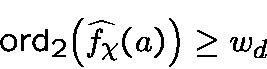
Moreover,is an idempotent whose weight is equal to the number of
such that equality occurs...
[PL, unpub.] Assume 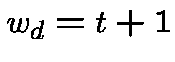 .
If the number of roots of .
If the number of roots of 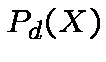 is less than
is less than 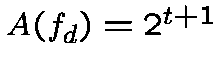 . . |
open problem : weight distribution of
![\begin{displaymath}\begin{split}\{0,1\}^m & \to \{0,1\}^{2m}\\x & \mapsto [x, -dx\mod n]\end{split}\end{displaymath}](img257.gif)