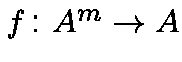NON-LINEARITY

Let $A^{}$ be a finite ring. The non-linearity of $f\colon A^m \to A$ is the Hamming distance between $f^{}$ and the space of affine functions.

$$d(f,g) = \sharp \{ x\in A^m \midf(x)\not=g(x)\}={\rm wt}(f-g)$$

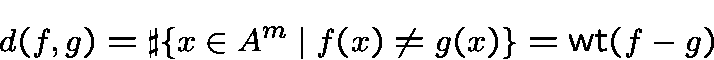
This notion applies in cryptography specially when $A^{}$ is the field of order $2$. The non-linearity of a boolean function$f^{}$ is given by

 

$$\delta(f) = 2^{m-1} - \frac 12 \sup_{a\in{\bf F}^{m}_2} \vert \widehat{f_\chi}(a)\vert$$

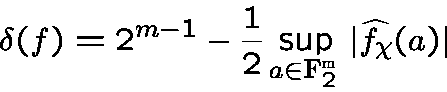
where $\chi$ is the non-trivial character of ${\bf F}_2$

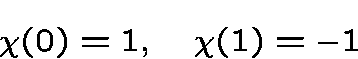
and $\widehat{f_\chi}$ is a Fourier coefficient of $f$.

$$\widehat{f_\chi}(a) = \sum_{x\in{\bf F}^{m}_2} f_\chi(x) \chi(ax).$$

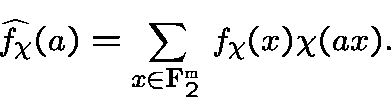
    One defines the spectral amplitude of $f$ and the spectral radius of order $m$

$$A(f) = \sup_{a\in{\bf F}^{m}_2} \vert \widehat{f_\chi}(a)\vert,\quadR(m) = \min_{f} A(f)$$

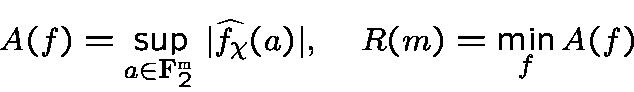
a boolean function $f$ such that $A(f)=R(m)$is called highly non-linear.

   What is the value of $R(m)$ ?
    Structure of highly non-linear functions ?