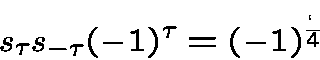Multiplier theorem for -perfect sequences
Belevitch [19xx]. Let 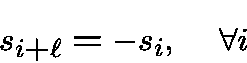 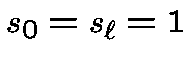 .
Let us set .
Let us set 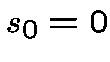 and
and 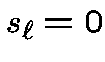 .
We obtain a sequence of type II of weight .
We obtain a sequence of type II of weight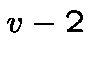 that satisfies
that satisfies
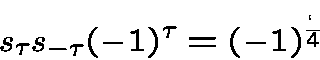
|
Assume
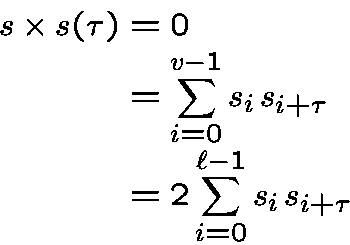
In the sum
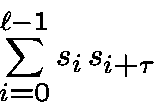
we have 2 terms equals toand
terms equal to
.The product of the non-zero terms is equal to
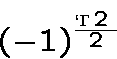
Let us replaceby
when
. For
,
appears twice except
and
which appears only once. Because of the signs the products of all the terms is equal to
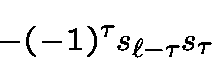
Finally,