Feuille de travaux pratiques numéro 7 cours d'algorithmique de licence

                                                   Ensembles Disjoints

Objectifs : implantation des ensembles disjoints,  composantes connexes.

Temps : 1 séance de 3 heures.

 

[ 0 ]  Rappels de cours.

L'algorithme générique COMPONNEXE(X,A) détermine les  composantes connexes d'un graphe  d'ensemble de sommets X et d'ensemble d'arêtes A.  Il est fondé sur l'emploi de la structure des ensembles disjoints  munie des opérations :

SINGLETON(s) :   Construit le l'ensemble {s}
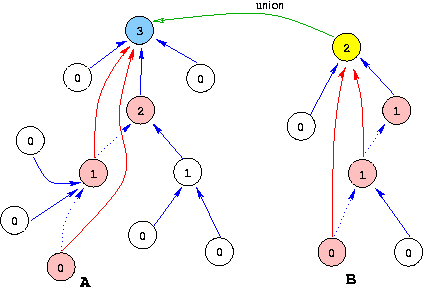
LEADER(x)    : Retourne le représentant de l'ensemble contenant le sommet  s.
UNION(x, y)  : Fusion des ensembles x et y.

ALGORITHME COMPONNEXES(X, A)
DONNEES   (X,A) : GRAPHE;
VARIABLE     ed : TABLEAU[X] ENSEMBLE;
              s : SOMMET;
            x,y : ENSEMBLE;
DEBUT
    POUR CHAQUE s DANS X FAIRE
         ed[s] := SINGLETON(s);
    FIP
    POUR CHAQUE (u,v) DANS A
         x := ED[ u ];
         y := ED[ v ];
         x := LEADER( x );
         y := LEADER( y );
         SI ( x != y ) ALORS
            UNION( x , y)
         FSI
    FIP
FIN

On sait que l'efficacité de l'algorithme dépend  du mode de représentation des ensembles : liste ou arbre, ainsique de certaines heuristiques : union pondérée, union par rang et compression de chemin. Dans les expériences numériques, nous utiliserons les graphes définis dans le TP précédent.

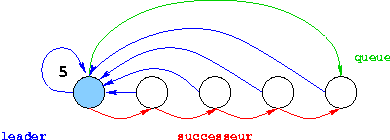
[ 1 ]  Représentation par des liste.

Il s'agit de chainer correctement une structure à  six  champs

struct  edliste { int valeur;
                  int cardinal;
                  struct edliste *leader, *succ, *queue;
                } ENRLISTE, *LISTE;

• Implanter la gestion des ensembles disjoints par liste chainée et union pondérée.
• Pour chaque entier n, calculer le nombre de composantes connexes du graphe G[n].
• préciser le nombre de charge prélevée.