Avril 1999
Dans la littérature, les matrices de Hadamard sont des matrices orthogonales dont les coefficients sont tous égaux à +1 ou -1. En d'autres termes, une matrice carrée H de dimension n est une matrice de Hadamard si le produit de H par sa transposée vaut n fois l'identité :
Ces matrices sont des objets de la combinatoire algébrique, une discipline des mathématiques discrètes qui s'applique notamment à certains domaines des télécommunications. La teminologie s'explique par la présence d'un article de Jacques Hadamard (1865-1963), mathématicien bien connu pour ses travaux sur les fonctions analytiques.
Etant donné un déterminant 
dans lequel on sait que les éléments sont inférieurs
en module à une quantité déterminée A,
il y a souvent lieu de chercher une limite que le module de 
ne puisse dépasser. À peu de choses près, c'est en
ces termes que débute l'article de J. Hadamard [8].
On peut supposer A=1, après nous avoir fait remarquer que
la majoration triviale 
à peu de chance d'être bonne, il utilise des propriétés 
bien connues 
du déterminant pour obtenir la majoration :
L'égalité a lieu si et seulement si les vecteurs lignes
sont deux à deux orthogonaux. La formule bien connue à laquelle
il fait allusion est la règle du révérend Charles
Lutwidge Dodgson (1832-1896) qui relie le déterminant 
à cinq de ses mineurs :
Une petite merveille de Lewis Carrol ! Je profite de l'occasion pour saluer le mathématicien internaute R. Chapman, et je le remercie de m'avoir signalé l'adresse de la home page de Doron Zeilberg. Vous y trouverez une élégante démonstration de la formule Alice.
Dans la littérature, les matrices de Hadamard à coefficients
complexes sont des matrices de Hadamard généralisées,
sont dites réelles, respectivement complexes, celles
qui sont à coefficients 
, respectivement dans l'ensemble des racines quatrièmes de l'unité.
Il n'est pas facile de préciser l'ensemble des valeurs de n
pour lesquelles il existe une matrice de Hadamard. L'initiateur de ces
questions, J. Sylvester (), avait déjà remarqué :
Par exemple, à partir de la matrice réelle
on construit la matrice de Hadamard
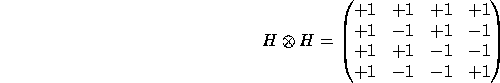
puis une matrice d'ordre 8, 16 etc... La multiplication d'une colonne ou d'une ligne par un nombre complexe de module 1, l'échange de deux lignes, l'échange de deux colonnes et la transposition engendre un groupe de transformations des matrices carrées qui ne change pas le caractère Hadamard d'une matrice. Deux matrices de Hadamard sont équivalentes si l'une s'obtient à partir de l'autre par une transformation de ce groupe. Sans perdre en généralité, on peut toujours supposer que les trois premières lignes d'une matrice de Hadamard réelle sont :
En particulier, mis à part les dimensions 1 et 2, la dimension d'une matrice de Hadamard réelle est un multiple de 4. Aujourd'hui, on sait construire des matrices de Hadamard réelles pour de nombreuses dimensions multiple de 4, voir les ouvrages [2][4]. Le lecteur en quête de célébrité devra s'attaquer à la
Elle est vérifiée pour les entiers strictement inférieurs
à 428, les autres valeurs
ouvertes
sont : 716, 764 etc... Une seconde merveille, attribuée parfois
à Jacques Hadamard , mais à tord puisqu elle ne figure pas
dans l'article précité. Dans un bref article, Raymond Paley
fournit un procédé de construction de matrices de Hadamard,
il ajoute :
seems probable that, whenever m is divisible by 4, it is possible
to construct an orthogonal matrix of order m composed of
, but the general theorem has every appearence of dificulty
Élève de Hardy et Littlewood à Cambridge, le jeune et brillant Raymond Paley disparaît tragiquement l'année de cette publication. À peine, agé de 26 ans, promis à une brillante carrière comparable aux mathématiciens qu'il cotoyait, parmi lesquels Littlewood, Zygmund, Pòlya et surtout Norbert Wiener qui écrit dans le mémoire [14] :
possessed of an extraordinary capacity for making friends and for scientific collaboration, Paley believed that the inspiration of continual interchange of ideas stimulates each collaborator to accomplish more than he would alone...
Un conseil à ne pas perdre de vue ! Continuons avec des choses plus techniques. Le lecteur qui ne serait pas familier avec les propriétés standards des corps finis risque d'être gêné, je lui suggère de lire une introduction sur les corps finis, ma note sur Gauss et la loi de réciprocité suffit largement.
Soient K un corps fini de caractéristique impaire, 
son caractère quadratique et R système de points projectifs
de l'espace 
. Le caractère est prolongé par 0 en 0. Pour tout couple
(x,y) de 
, on a :
En effet, on commence par remarquer que la somme ne dépend pas
de R. Si x=y, il n'y a rien à faire sinon,
il existe un automorphisme de
qui envoie permet de se ramener au cas 
et 
, et là tout est limpide.
On construit alors la matrice de Paley 
qui est orthogonale sans être Hadamard puisque les coefficients de
la diagonale sont tous nuls. Dans la terminologie de Belevitch, il s'agit
d'une matrice de conférences car elle permet de définir un
protocole de communication partagée sur une même ligne téléphonique.
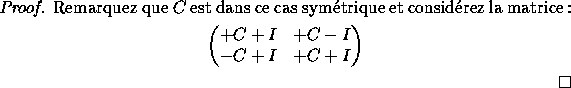
Les deux théorèmes précédents constituent des constructions primaires à partir desquelles d'autres matrices de Hadamard pourront être construites. Le produit de Kronecker (produit tensoriel) n'est pas le seul outil. Ci-dessous suivent des résultats parmi les plus importants extraits du survey de Jennifer Seberry et Mieko Yamada, chapitre 11 de [4] dans lequel vous ne trouverez pas l'approche assez inattendue de Horadam et De Launey [9] dans laquelles les auteurs explorent les propriétées d'orthogonalité des matrices cocycliques construites à partir de certains système de facteurs.
Un ensemble de Willamson d'ordre n est un ensemble de quatre
matrices A, B , C et D, à coefficients
, de dimension n satisfaisant aux condittions :
Soient 
, 
,.. 
des entiers, 
, 
,... 
des indéterminées qui commutent deux à deux et n
un entier. Une configuration orthogonale de type 
est une matrice X à coefficients dans 
vérifiant :
Par exemple, la matrice :
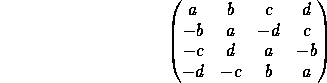
définit une configuration orthogonale OD(4; 1,1,1,1). Une configuration remarquable utilisée par Léonard Euler dans ses travaux sur la décomposition des nombre en somme de 4 carrés.
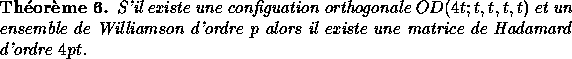
En faisant des hypothèses supplémentaires sur la forme de la matrice, on peut contrarier la conjecture de Paley. Les travaux de Turyn [13, 12], Eliahou et Kervaire [5] et Schmidt [11] suggèrent la :
vérifiée pour des ordres voisins de 100,000, cette conjecture
est un cas particulier de la conjecture de Ryser sur la non-existence de
certains ensembles de différences...
