![]() there exists examples of constructions of sequences from the Galois
rings
there exists examples of constructions of sequences from the Galois
rings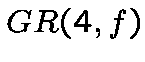 [
Sole, Boztas, Kumar, 1994]
[
Sole, Boztas, Kumar, 1994]
I use Gauss sums over finite semi-simple algebras to give the divisibility and the weight of abelian codes [PL, 1998].
there exists examples of constructions of sequences from the Galois rings
[ Sole, Boztas, Kumar, 1994]
We may hope new results replacing the finite fields by finite rings.
They are complete Gauss sums
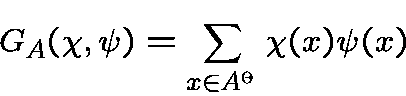
and incomplete Gauss sums
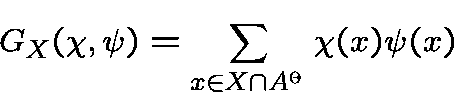
whereis a subgroup of
. For applications in designs theory there is no restriction on
but for sequences point of view
must be cyclic. Namely, if
is local there are Techmüller Gauss sums.
The evaluation of Gauss sums is not easy on finite field and harder on finite rings but there are good news :
Local Frobenius ring : the modulus of complete Gauss is easy calculate [PL, 1998].
Galois rings : The Teichmüller Gauss sums are well understand in terms of curves [KHC, 1996].
Galois rings of characteristic have like Stickelberger's congruences properties, [PL, 1998].
Ramified rings : good family of sequences can be construct from such rings, [PL, 1998]. for example :
![\begin{displaymath}B = GR(4, f)[X]/(X^2-2, 2X)\end{displaymath}](img266.gif)