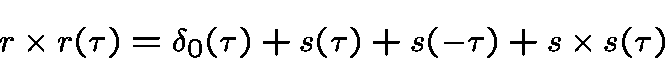Multiplier theorem for-perfect sequences
Belevitch [19xx]. Let 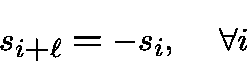 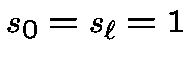 .
Let us set .
Let us set 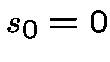 and
and 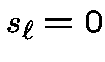 .
We obtain a sequence of type II of weight .
We obtain a sequence of type II of weight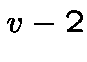 that satisfies
that satisfies
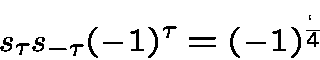
|
Assume
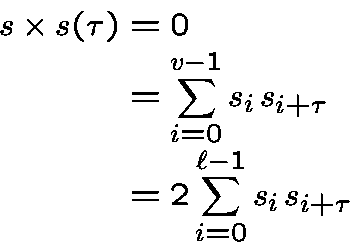
In the sum
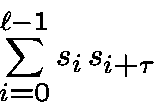
we have 2 terms equals toand
terms equal to
.The product of the non-zero terms is equal to
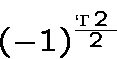
Let us replaceby
when
. For
,
appears twice except
and
which appears only once. Because of the signs the products of all the terms is equal to
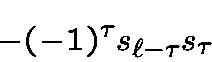
Finally,
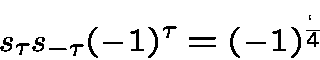
Transformation of Legendre sequences
Ifthen we can tranform the Legendre sequence
in a binary sequence
by
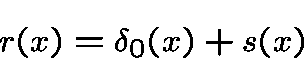
the out-phase correlations are unchanged since