GAUSS SUMS

Let $L$ be a finite field.
$\chi$  a multiplicative character
$\psi$ be an additive character.
The Fourier transform of$\chi$ in $\psi$ is the Gauss sum

$$G_L(\chi,\psi) =\sum_{x\in L^\times} \chi(x)\psi(x)=\hat \chi(\psi).$$

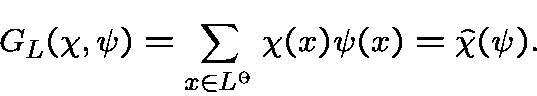
    of module , if both of$\chi$ in $\psi$ are not trivial.

Jacobi sums $\leftrightarrow$    convolution

    The size of the instersection of a subgroup $G$ of ${L}^\times$ with the hyperplan $${\rm tr}_{{L}/{K}}(ax) = c \not=0$$ is given by CSM and PF

$$\frac {\vert G\vert}q + \frac{\vert G\vert}{q(q^f-1)} \sum_{\chi\inG^\bot}G_{L}(\chi,\mu_L)G_K(\bar\chi)\chi(c/a)$$

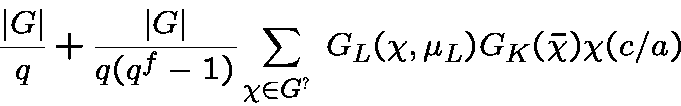
    starting point of my papers in (irreducible) cyclic codes that I have adapated in the context of abelian codes defining Gauss sums over semi-simple algebras.