

Next:LEGENDRE
SEQUENCES Up:Les
sommes de caractères Previous:SEQUENCES
MAXIMAL SEQUENCES
Let 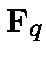 be a finite extension of
be a finite extension of 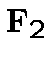 .
.
Let 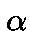 be a primitive root of
be a primitive root of 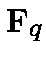 .
.
 The binary sequence of period
The binary sequence of period 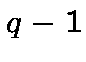 ,
,
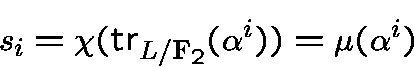
has small periodic autocorrelation.
 Indeed,
Indeed,
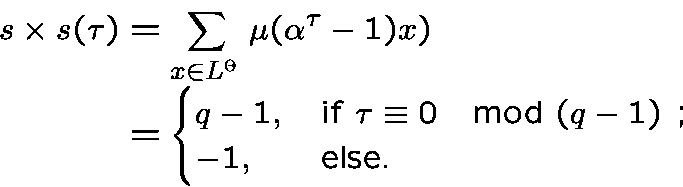
 very algebraic !
very algebraic !


Next:LEGENDRE
SEQUENCES Up:Les
sommes de caractères Previous:SEQUENCES
Philippe Langevin
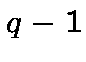 ,
,be a finite extension of
.
be a primitive root of
.
The binary sequence of period
,
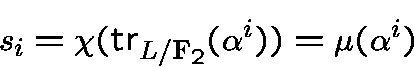
Indeed,
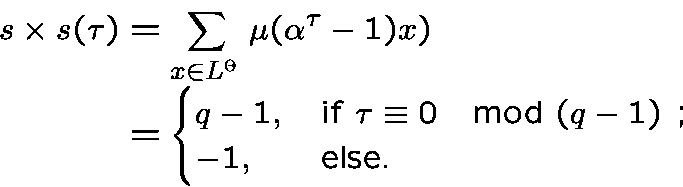
very algebraic !