LEGENDRE SEQUENCES

Let $p$ be a prime number,
the ternary sequence $s$

$$s_i = \genfrac{(}{)}{1pt}{}{i}{p} =\begin{cases}+1, & \tex...... $i=0$;}\\-1, & \text{if $i$ is not a square;}\\\end{cases}$$

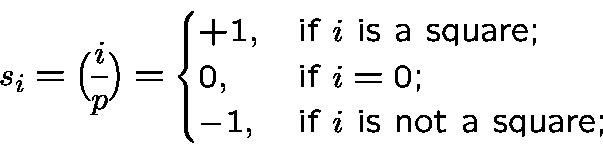
has also small periodic correlation.

    Once more the reason is essentially algebraic.

    Note that $\genfrac{(}{)}{1pt}{}{p}{q}$ is the symbol of Legendre (1752-1833). In a certain sense, the fundations of the present work are in the XVIII  : Fourier, Gauss and Poisson.