AlMOST PERFECT SEQUENCES

    The main conjecture in the theory of sequences says that Perfect binary sequences do not exist. Too bad ! they would be useful.

To avoid this obstruction, we look for ternary sequences i.e. symbols are $-1, 0, +1$ with perfect correlations, or binary sequences with almost perfect correlations.

$$f\times f(z)=\begin{cases}v,&\text{if $z=0$ ;}\\4\th......xt{if $z=\frac{v}{2}$ ;}\\0,&\text{else.}\\\end{cases}$$

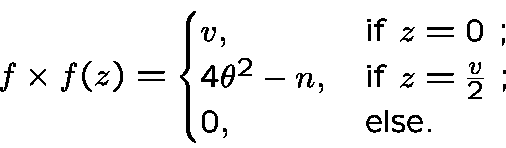
    These are the $\theta$-almost perfect sequences of J. Wolfmann. The length of a $\theta$-APS must be a multiple of $4$.

$\theta=1$ In his paper, J. Wolfmann finds $1$-APS for all the multiple of $4$$\leq 100$ except for 6 specials values values $32$, $44$, $68$, $72$, $80$, $92$. I have explained why, [PL, 1993]. Th

Belevitch  multiplier theorem

$\theta=0$     There is no $0$-APS .

proof

$\theta=2$ Only three lengths for $2$-APS are known and there is no more such sequences up to length $100$. [Arazu, 1997].

$\theta>2$ nothing is known !  excepted some non-existence criterions [PL,  94]