FOURIER TRANSFORM I

Let $s$ be a sequence of period $v$, the Fourier transform of $s$ at the point $u$ is defined by

$$\hat s( u) = \sum_{j=0}^{n-1} s(j) \zeta^{ju}_n,\qquad \zeta_n = \exp(2i\pi /n).$$

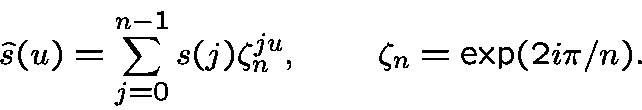
    We refind the sequence $s$ by the inversion formula

$$s(v) ={1\over n} \sum_{j=0}^{n-1} \hat s(j) \zeta^{-jv}_n$$

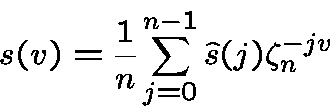
    Moreover, the correlation of $s$satisfies

$$\widehat{s\times s}(u) = \vert \hat s(u) \vert{}^2$$

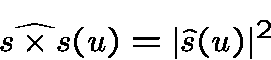
    back to the Legendre sequences,

$$\hat s(u) =\sum_{j=0}^p \genfrac{(}{)}{1pt}{}{j}{p} \zeta_p^{ju} =\genfrac{(}{)}{1pt}{}{u}{p}G_{{\bf F}_p}(\nu)$$

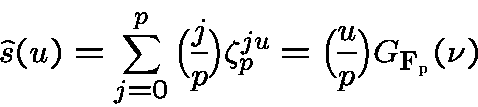
        which since Gauss has magnitude 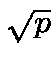$\sqrt{p}$, if $u\not=0$.
 
 

$$s\times s(v) = {1\over p} \sum_{j=1}^{p-1} p\,\zeta^{-jv}_n= -1$$

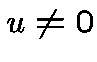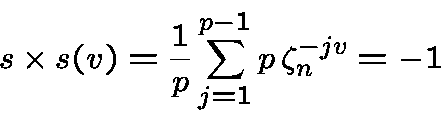
    The contribution of Gauss is deeper. He spent many years to prove the nice formula :

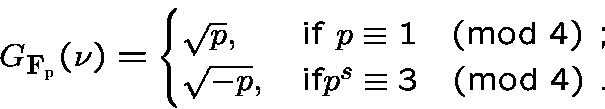$$G_{{\bf F}_p}(\nu)=\begin{cases}\sqrt{p},&\text{if $p \equiv......\sqrt{-p},&\text{if$p^s\equiv 3\pmod4$ .}\\\end{cases}$$ (1)

 

the key point of sign determination is a relation obtained considering Gauss sums as eigenvalues of the Fourier transform.

$$(-1)^{{p - 1}\over {2}} p^{{p - 3}\over{2}} G_{{\bf F}_p}(\nu......{2}}\prod_{1\leq i<j\leq p-1}\sin\big({(j-i)\pi\over p}\big)$$

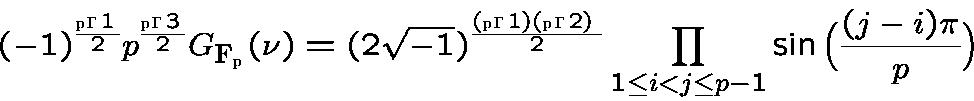
    The evaluation of some Gauss sums represents the mathematical part of my work ( and those of O.Mbodj ). It is an application of Galois theory and cyclotomic the fields.