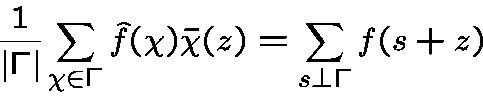

Next:GAUSS
SUMS
Up:Les
sommes de caractères
Previous:FOURIER
TRANSFORM I
FOURIER TRANSFORM II
Because of analysis, everybody knows the Fourier
transform
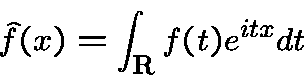
It has an algebraic analog
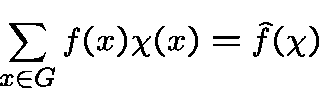
A character 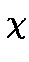 of
of 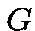 is an homorphism from the group
is an homorphism from the group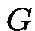 into
into 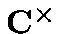
 orthogonality relation
orthogonality relation
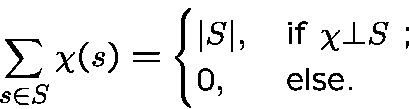
 Character sums method.
Character sums method.
Let 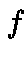 be a mapping from
be a mapping from 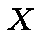 into
into 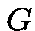 ,
the number
,
the number 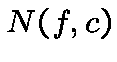 of solutions of
of solutions of 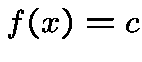 in
in 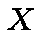 is given by
is given by
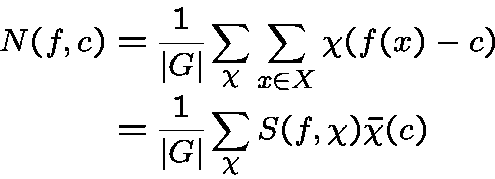
 Trivialisations.
Trivialisations.
Let 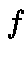 and
and 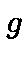 the product of convolution of
the product of convolution of 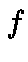 by
by 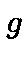
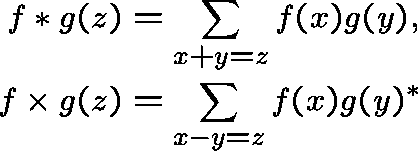
the fourier transform is an homomorphism
from ![${\bf C}[G]$](img147.gif) into
into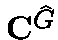
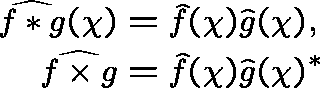
 Poisson Formula.
Poisson Formula.
Let 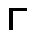 be a subgroup of
be a subgroup of 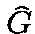
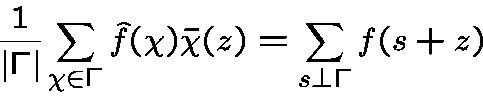
simple but useful !
-
McWilliams formula
-
McEliece weight formula
-
Multiplier theorem of Hall -Turyn
-
degree of bent functions
-
etc...


Next:GAUSS
SUMS
Up:Les
sommes de caractères
Previous:FOURIER
TRANSFORM I
Philippe Langevin
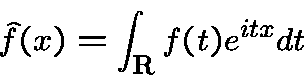
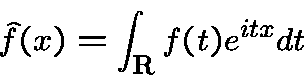
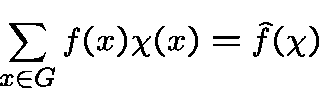
of
is an homorphism from the group
into
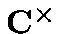
orthogonality relation
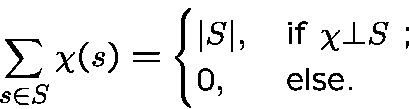
Character sums method.
be a mapping from
into
, the number
of solutions of
in
is given by
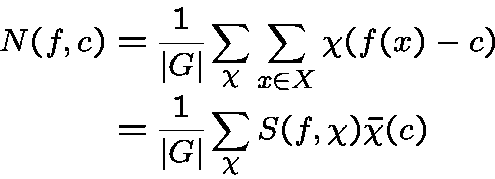
Trivialisations.
and
the product of convolution of
by
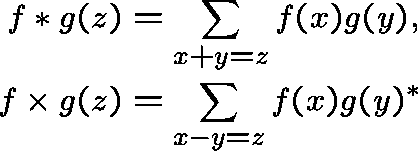
into
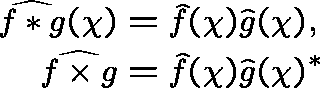
Poisson Formula.
be a subgroup of