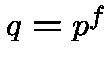
Let
Any prime ideal ![]() above
above ![]() in the ring
in the ring 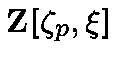 offers a representation of the field
offers a representation of the field ![]()
Letbe a prime, let
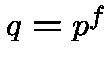
Let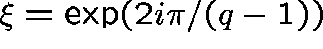
Any prime ideal
above
in the ring
offers a representation of the field
![\begin{displaymath}{\bf F}_q\sim {\bf Z}[\zeta_p,\xi]/ \wp\end{displaymath}](img215.gif)
The multiplicative characterof
defines by
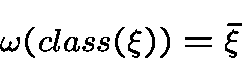
has order.
[Stickelberger, 1890]
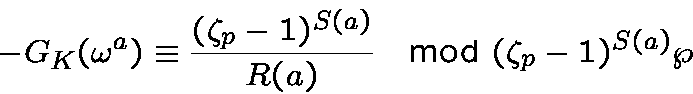
whereand
. The
are the
-digits of
.
divisibility of abelian codes
regular section groups
BWD-codes
Determination of Gauss sums