BOUNDS

    Parseval bound.

$$\sum_{a\in{\bf F}^{m}_2} \widehat{f_\chi}(a)^2 = 2^{2m}\Rightarrow R(m) \geq 2^{m/2}$$

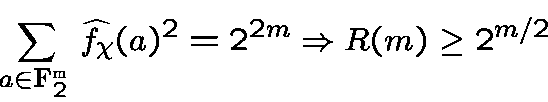
    Quadratic bound Let $q$ be a quadratic form.$$\widehat{q_\chi}(a)^2 = \epsilon(a)\,2^{\frac{m+k}2}\Rightarrow R(m) \leq 2^{{\lceil{\null m/2}\rceil}}$$

where $\epsilon(a) \in \{-1,0,1\}$.

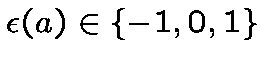    Note that if $m$ is even then $R(m)= 2^{m/2}$, and highly non-linear functions are called bent functions.

    In the odd case $R(m)$ is unknown when $m\geq 9$.
I say that $f$ exceeds the quadratic bound if

$$A(f) < 2^{{\lceil{m\over 2}\rceil}}$$
 

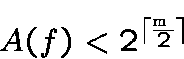
[Paterson and Wiedeman, 1981] There exists functions with 9 variables that exceeds the quadratic bound.

    the main conjectures are

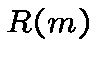$R(m)$ is even , and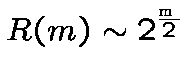 $R(m) \sim 2^{m\over 2}$

• urcosets of odd weights.
• action of ${\rm GL}({{\bf F}_2},m)$, with J.-P. Zanotti.
• non-linearity of cubics, with P. Solé, and X.-D. Hou.
• generation and structure of bent functions, with X.-D. Hou
• derivation, index and height.
• etc...

[PL, 1991] A cubic with 9 variables does not exceed the quadratic bound.

proof ?
Ax theorem implies that $\widehat{f_\chi}(a)$ is a multiple of $2^{{\lceil{m\over 3}\rceil}}$

+ Poisson formula.