AX THEOREM

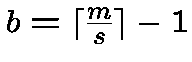[Ax, 1964] Let $K$ be a finite field of $q$ elements. Let $f$ a polynomial of degree $s$ in $K[X_1,X_2,\dots, X_m]$. The number of zeros of$f$ is divisible by $q^b$ where $b={\lceil{\frac ms}\rceil} - 1$.

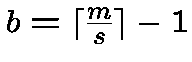This is a strong improvement of the Chevalley theorem. The main ingredient of the proof is a famous relation of Stickelberger (1890) about congruences satisfy by the Gauss sums.

An investment in character theory, Gauss sums, and cyclotomy is necessary to follow the proof.

I did... and it has been fruitfull !