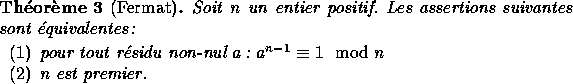Soient a et b deux entiers naturels, b;SPMgt;0. Il existe un unique couple d'entiers naturels (q,r) vérifiant :
Effectuer la division Euclidienne de a par b, c'est trouver le quotient q et le reste r satisfaisant aux conditions (2). La notion de division à reste minimal est moins populaire, sous les mêmes conditions, il existe un unique couple (q,r) d'entiers relatifs vérifiant :
Effectuer la division à reste minimal de a par b, c'est trouver le quotient q et le reste r satisfaisant aux conditions (3)
Soit n un nombre entier positif. L'ensemble des entiers relatifs est
muni d'une relation dite de congruence. L'entier x est congru à y
modulo n si et seulement si n divise y-x, on écrit 
; c'est une relation d'équivalence compatible avec les lois d'addition et de multiplication. Un entier compris entre 0 ert n-1 est un résidu modulo n. Pour tout couple de résidus (x,y) on note 
et 
les résidus définis par :
L'ensemble des résidus modulo n muni de ces deux lois constitue un
anneau fini, commutatif et unitaire; généralement noté 
: c'est un
anneau ``quotient''.
Il résulte de cette proposition que si n est premier alors le nombre
de solutions de l'équation 
est au plus d. Remarquez que l'équation 
possède 4 solutions dans 
!
