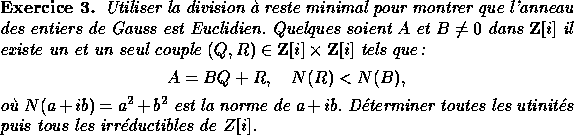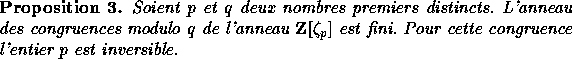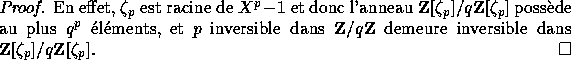Soient p et q deux nombres premiers impairs. La loi de réciprocité quadratique énoncée par Legendre mais prouvée par Gauss affirme :
où 
vaut -1 si et seulement si
p et q sont congrus à 3 modulo 4.
Il existe plus d'une centaine de preuves. La preuve de Reichardt, exposée dans [2], est assez remarquable : basée sur le lemme de Gauss, elle n'utilise absolument pas la notion d'extension algébrique. La démonstration proposée repose sur les sommes de Gauss et les congruences généralisées aux anneaux entiers cyclotomiques. Elle constitue une introduction à la théorie algébrique des nombres. Pour des approfondissement, voir incontournable ouvrage de P. Samuel [3].
Le notion de congruence se généralise à tous les sous-anneaux du corps des nombres complexes. Dans un tel anneau A, pour tout entier q, nous écrirons encore
pour exprimer que q divise la difference x-y. C'est une relation
d'équivalence compatible avec les lois d'addition et de multiplication ce qui permet de définir la notion d'anneau résiduel : A/qA. Considérons l'anneau des entiers de Gauss 
, chaque éléments 
se sécompose d'une et une seule manière comme z= a+ib, où a et b sont deux entiers. Il en résulte que l'ensemble des nombres a+ib en faisant varier les entiers a et b dans l'ensemble des résidus modulo q forme un système de représentant de 
et donc que cette anneau contient 
éléments. Le lecteur profitera de l'occasion pour étudier les anneaux :
Il remarquera que le premier anneau est ``nilpotent'', que le troisième est ``réduit'' et que le deuxième est un corps à 9 éléments, extension de degré 2 de 
, c'est un corps fini non premier :
un ``corps de Galois''.
