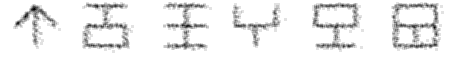Quelques Problèmes Pour Insomniaques

La liste de mes casse-têtes est issue d'une
sélection assez sévère. Je les ai receuillis au cours de ces
fameux banquets qui terminent les colloques, au cours d'une pause café...
Il vous faudra utiliser beaucoup de votre temps libre pour parvenir à les résoudre.
Ils constituent un remède idéal pour lutter contre le ramollissement
ancéphalique !
Vous souffrez d'insomnies ?
Ils ne vous vous guériront
pas de cette terrible maladie mais
ils seront de bons compagnons pour
vos nuits difficiles.
Bonne chance a tous !
- niveau X
- niveau 0
- Les tas de pieces,
un énoncé classique communiqué
par Guénael Renault. Colloque C2 du GDR-IM, Fréjus (2009).
- Le lemme des cinq,
un petit problème pour les collégiens communiqué par Youssef Ouknine
de passage à l'institut de mathématiques de Toulon au cours de l'automne 2019.
- niveau 1
- niveau 2
- Le test de Landau Communiqué par autour d'une
partie de billard à Badwindheim !
- Quine Une petite bizarrerie informatique communiquée par Daniel Augot,
surprenant !
- niveau 3
- Des billes de couleurs Inspiré d'un problème d'un
ancien
concours Jeux et Strategies que j'ai perdu de vue...
- Le trés classique problème des 12 pièces
communiqué par Michel Bonnafous entre deux rondes de N2 !
- niveau 4
- niveau 5
- niveau 6
- Un problème sur points et droites
du plan proposé dans l'introduction d'une conférence de
Terence Tao. Il
existe une solution élémentaire qui a complétement échappé au célèbre
mathématien Paul Erdöz.
- niveau 7
- Recouvrement du disque,
un redoutable problème proposé par Marc Perret à lors
d'un des premiers des AGCT de Luminy,
techniquement à la portée d'un bachelier...
- niveau X
- dissection pyramidale. Une question sur les
carrés dont j'ai découvert l'existence en 2019. Il mélange deux problèmes
du début de 20e siècle l'un sur la dissection du carré, l'autre sur les
tas de boulets de canon. En attente d'une solution
élégante pour devenir classique!
dissection pyramidale
Le nombre pyramidal carré compte le nombre de boulets de canons
disposés en couches carrées. Les premiers nombres pyramidaux sont :
1, 5, 14, 30 etc... Le gentil lecteur doit se convaincre (pas facile)
que 1 et 4900 sont les deux seuls carrés qui sont des nombres pyramidaux carrés.
1 + 2^2 + 3^2 + ... + 24^2 = 4900 = 70^2.
Mézalors,
pensez vous qu'il soit possible de partitioner une surface
carrée 70x70 avec les 24 surfaces carrés 1x1, 2x2, 3x3, ..., 24x24?
Quine informatique
Les quines informatiques sont des programmes, en voici une :
char *p="char *p=%c%s%c;main(){printf(p,34,p,34);}";main(){printf(p,34,p,34);}
Alors, un quine, c'est quoi ?
Lemme des cinq
On place cinq points dans un carré de côté 1.
Montrer que deux de ces points sont à une distance moindre que 3/4.
Indication : rien à voir avec le classique lemme des cinq !
Tas de pieces
Soient 10 tas de 10 pieces de monnaies. Les fausses pieces pesent 10 grammes, les
vraies pieces 20 grammes. Un des tas ne contient que des fausses pieces, les autres
uniquement des vraies.
Comment déterminer le tas de fausses pieces en une pesée ?
Indication : difficulté... aucune !
La fausse pièce de monnaie
Il y a 12 pièces. L'une d'elle est fausse, les autres sont
authentiques et parfaitement identique en masse. On sait
que les masses d'une fausse et d'une vraie pièces diffèrent.
Comment déterminer la fausse pièce à l'aide d'une balance
en précisant si cette dernière est plus légère ou plus lourde
qu'une vraie. Il s'agit de minimiser le nombre de pesées.
Indication : entropie.
Ballade des cavaliers.
En suivant les règles habituelles du jeu d'échecs,

comment passer de la position de gauche vers la position de droite ?
Indication : il suffit de changer de point de vue.
La suite de Landau.
On raconte que le physicien Landau avait pour
habitude de tester les candidats doctorants avec
des suites de symboles mystérieux...
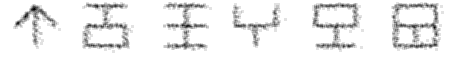
Quel est le symbole à suivre ?.
Indication : sans.

Une boîte de billes
Une boite à chaussures contient 168
billes
de différentes couleurs : des billes rouges, des billes orange
et
des billes jaunes. Il y a 10 fois moins de billes rouges
que d'oranges, et 5
fois
plus de rouges que de jaunes.
Determiner le
nombre
de billes rouges.
Indication : 15 n'est pas la solution...

Pavage du carre.
On pave un carré avec des rectangles.
Ne
pas confondre pavage et recouvrement, voir les figures. On suppose que
chaque rectangle possède au moins un côté de
longueur
entière. Le nombre de rectangles est donc fini.
Montrer que le côté du
carré
est de longueur entière.
Indication : vous pouvez remplacer carré par rectangle !

Recouvrement du Disque.
Un disque dont le diamètre mesure 1
unité
est recouvert par un nombre fini de rectangles.
Montrer que la sommes des largeurs
des
rectangles est superieure à 1.
Indications : la solution vient de l'espace : sphères, projections...
Communiqué par Marc Perret...

tas de galets.
Sur la plage de la
batterie basse, j'ai récolté des galets, un nombre impair
de galets. L'ensemble de galets possède une
propriété remarquable : quel que soit le galet mis de
côté, il existe toujours un moyen de disposer les autres
sur les deux plateaux d'une balance de sorte à conserver
l'équilibre en masse et en nombre.
Montrer que tous les galets sont de
même masse.
indication
: un corps à deux éléments.
Communiqué
par Eric Brier...
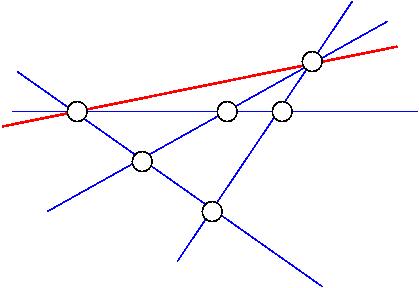
points et droites.
On considère un nuage de points non alignés dans le plan réel.
Montrer qu'il existe une droite qui passe uniquement
par seulement deux de ces points.
indication : l'énoncé est faux sur un plan général.
vu sur la toile...
alignement, encore et encore.
On considère un ensemble fini de points dans le plan réel. Toutes
droites passant par deux de ces points est incidente à un troisième.
Montrer que les points sont alignés.
indication : l'énoncé est faux sur un plan général.
vu sur la toile...
[Contacts]
[home page]
[Laboratory]
[Department]
[University]
Philippe Langevin, Novembre 1998.
dernière modification : été 2014.