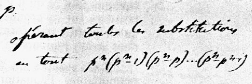Le testament de Galois

     Evariste Galois est célèbre pour la théorie qui porte son nom : la théorie de Galois. Une théorie élégante, riche et féconde qu'il invente au cours de ses recherches sur la résolution des équations algébriques et qu'il nous lègue dans  son fameux testament. D'après la légende, une coquette prénomée Stéphanie  serait à l'origine d'un différent entre le précoce génie des mathématiques et un officier. Les deux hommes défendirent  leurs honneurs  dans un duel aux  pistolets qui fût fatal à Galois...  Les travaux de Galois furent plutôt mal traités par l'Académie des sciences. Un premier manuscrit de Galois sera perdu par Fourier. Poisson ne trouvera rien de novateur  dans le second, probablement pour des raisons (bassement) politiques : de quoi perturber n'importe quel jeune chercheur, non ?

            1.   La lettre testament
            2.    L'école italienne
            3.    Ruffini, Abel et Galois
              4.    Galoiseries
            5.    Les corps imaginaires de Galois
            6.    La théorie de Galois en quelques mots
            7.    Obstruction du cinquième degré
            8.    Equation du second degré à la Galois
            9.    Equation du troisième degré à la Galois
            A.   Troisième degré : la méthode de Tartaglia
            B.   Quatrième degré à la Galois
            C.   Quatrième degré : la méthode de Ferrari
            D.    Liens et références

1. La lettre testament

J'ai fait en analyse plusieurs choses nouvelles. Les unes concernent la théorie des équations algébriques; les autres, les fonctions intégrales.

Dans la théorie des équations, j'ai recherché dans quels cas les équations étaient résolubles par des radicaux ; ce qui ma donné occasion d'approfondir cette théorie, et de décrire toutes les transformations possibles sur une équation, lors meme qu'elle n'est pas résoluble par radicaux.

On pourra faire avec tout cela trois Mémoires.

Le premier est écrit; et, malgré ce qu'en a dit Poisson, je le maintiens avec les corrections que j'y ai faites.

Le second contient des applications assez curieuses de la théorie des équations. Voici le résumé des choses les plus importantes.

1* D'après les propositions II et III du premier Mémoires, on voit une grande différence entre adjoindre à une équation une des racines d'une équation auxiliaire, ou les adjoindre toutes.

Dans les deux cas, le groupe de l'équation se partage par l'adjonction en groupes tels que l'on passe de l'un à l'autre par une meme substitution; mais la condition que ces groupes aient les memes substitutions n'a lieu certainement que dans le second cas. Cela s'appelle la décomposition propre.

En d'autres termes, quand un groupe G en contient un autre H, le groupe G peut se partager en groupes, que l'on obtient chacun en opérant sur les permutations de H une meme substitution ; en sorte que  G = H + H S + H  S' + ... Et aussi, il peut se décomposer en groupes qui ont toutes les memes substitutions G = H + T H + T' H + ... Ces deux genres de décompositions ne coincident pas ordinairement. Quand elles coincident, la décomposition est dite propre.

Il est aisé de voir que quand le groupe d'une équation n'est susceptible d'aucune décomposition propre, on aura beau transformer cette équation, les groupes des équations transformées auront toujours le meme nombre de permutations.

Au contraire, quand le groupe d'une équation est susceptible d'une décomposition propre, en sorte qu'il  se partage en M groupes de N permutations, on pourra résoudre l'équation donnée au moyen de deux équations : l'une aura un groupe de M permutations, l'autre un de N permutations.

Lors donc qu'on aura épuisé sur le groupe d'une équation tout ce qu'il y a de décompositions propres possibles sur ce groupe, on arrivera à des groupes qu'on pourra transformer, mais dont les permutations seront toujours en meme ordre.

Si ces groupes ont chacun un nombre premier de permutations, l'équation sera soluble par radicaux; sinon non.

Le plus petit nombre de permutations que puisse avoir un groupe indécomposable, quand ce nombre n'est pas premier est 5.4.3.
2* Les décompositions  les plus simples sont celles qui ont lieu par la méthode de M. Gauss.
Comme ces décompositions sont évidentes, meme dans la forme actuelle du groupe de l'équation, il est inutile de s'arreter longtemps sur cet objet.
Quelles décompositions sont praticables sur une équation qui ne se simplifie pas par la méthode de M. Gauss ?
J'ai appelé primitives les équations qui ne peuvent pas se simplifier par la méthodes de M. Gauss ; non que ces équations soient réellement indécomposables, puisqu'elles peuvent meme se résoudre par radicaux. Comme le lemme à la théorie des équations primitives solubles par radicaux, j'ai mis en juin 1830, dans le Bulletin Férussac, une analyse sur les imaginaires de la théorie des nombres.
On trouvera ci-jointe la démonstration des théorèmes suivants.

1. Pour qu'une équation primitive soit soluble par radicaux, elle doit etre de degré p^v, p étant premier.

2. Toutes les permutations d'une pareille équation sont de la forme

x_k.l.m... / x_ak +bl + cm + ... + f.  x_a1k +b1l + c1m + ... + g.  ...

k,l,m ... étant v indices, qui , prenant chacun p valeurs, indiquent toutes les racines. Les indices sont pris suivant module p ; c'est-à-dire que la racine sera la meme quand on ajoutera à l'un des indices un multiple de p.
 

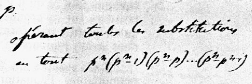
Le groupes qu'on obtient en opérant toutes les substitutions de cette forme linéaire contient en tout p^n (p^n-p) ...(p^n-p^n-1) permutations. Il s'en faut que dans cette généralité les équations qui lui  répondent sont résoluble par radicaux. La condition que j'ai indiquée dans le Bulletin de Férussac pour que l'équation soit résoluble par radicaux est trop restreinte ; il y a peu d'exceptions, mais il y en a. La dernière application de la théorie des équations est relative aux équations modulaires des fonctions elliptiques.

    [ ... ]
 
 

Tu sais mon cher Auguste, que ces sujets ne sont pas les seuls que j'aie explorés. Mes principales méditations, depuis quelques temps, étaient dirigées sur l'application à l'analyse transcendante de la théorie de l'ambiguité. Il s'agissait de voir a priori, dans une relation entre des quantités ou fonctions transcendantes, quels échanges on pouvait faire, quelles quantités on pouvait substituer aux quantités données, sans que la relation put cesser d'avoir lieu. Cela fait reconnaitre de suite l'impossibilité de beaucoup d'expressions que l'on pourrait chercher. Mais je n'ai pas le temps, et mes idées ne sont pas encore bien développées sur ce terrain, qui est immense.

Tu feras imprimer cette lettre dans la Revue encyclopédique. Je me suis souvent hasardé dans ma vie à avancer des propositions dont je n'étais pas sûr. Mais tout ce que j'ai écrit là est depuis bientôt un an dans ma tête, et il est trop de mon intérêt de ne pas me tromper pour qu'on me soupconne d'avoir énoncé des théorèmes dont je n'aurais pas la démonstration complète. Tu prieras publiquement Jacobi et Gauss de donner leur avis, non sur la vérité, mais sur l'importance des théorèmes. Après cela, il y aura, j'espère, des gens qui trouveront leur profit à déchiffrer tout ce gachis. Je t'embrasse avec effusion.

E. Galois, le 29 mai 1832  

    Evariste Galois meurt de ses blessures quelques jours avoir écrit ce texte. Jamais ces lignes  ne parviendront au grand Carl Friederich Gauss qui ignore l'existence du jeune mathématicien. Légende ou pas, les initiales  S. D. apparaissent dans l'une des sept pages du manuscrit. Les ratures et les surcharges témoignent de la fébrilité du jeune qui va mourir, et du génie qui transmet  les clefs d'un  savoir inconnu mais capital.  La lettre originale est conservée à la bibliothèque de l'Institut. Il est composé de sept pages que j'ai scannées pour vous à partir de la publication de l'A.P.M.E.P numéro 48, année 1982 qu'il faut consulter pour les détails et commentaires.
 

      Dans ces pages, il expose ses idées sur la résolution des équations algébriques. Des idées brillantes qui jettent un pont entre la théorie des groupes et la théories des extensions algébriques. Deux théories naissantes qui deviendront fondamentales quelques décennies plus loin.
 

2.    Ecole italienne

x = [ - b + RQ[ b^2 - 4 a c] ] est composée des coefficients de l'équations d'un terme radical qui avec d'autres formules concernant les équations bicarrées constituent un modèle de recherche pour les équations de degré plus élevé. Au début, du XVI-ième Scipion del Ferro donne l'expression de certaines racines de l'équation du troisième degré T^3 + a T = b à partir de radicaux quadratiques et cubiques.
 
 

RC[ b/2 + RQ [ (b/2)^2 + (a/3)^3] ] + RC[ b/2 -RQ [ (b/2)^2 + (a/3)^3] ]
 
 

Cardan et Tartaglia vont généraliser les résultats de Scipion del Ferro. Ils font tomber le terme du second degré de l'équation aT^3 + bT^2+cT+d pour obtenir une équation du type précédent. Pour pouvoir faire fonctionner ce type de formule dans le cas où [ (b/2)^2 + (a/3)^3] est négatif, ils inventent les nombres imaginaires +ipiu de meno et -i meno de meno dont les règles d'utilisations seront décrites par Bombelli un des disciples de Cardano qui montre que :
 
 

Le cas du troisième degré vient juste de tomber quand Ludovico Ferrari, un second disciple de Cardan, ramène la résolution du degré 4 à celle du degré 3 en effectuant un changement de variable T = X^2 + Z dans T^4 = aT^2 + b T + c de sorte à faire apparaître un carré parfait, ce qui donne pour Z une relation du troisième degré.
 
 

    Après quoi, les algébristes tenteront très naturellement de résoudre l'équation du cinquième degré à l'aide de radicaux et autres équations auxiliaires. Quelques progrès seront engrangés par Viète qui donne l'expression des coefficients d'une équation à partir de ses racines. Puis, Girard qui affirme qu'une équation de degré n possède exactement n racines, à condition de compter les multiplicités. La résolution des équations algébriques marque une pose malgré les tentative de Tschirnhaus, Leibnitz et Euler! Les formules de Cote et De Moivre sur l'expression des racines de l'unité constituent la dernière avancée de cette période et permettront à la Lagrange d'exprimer ses résolvantes.

    A la fin du XVIII-ième, Lagrange étudie la question de résolubilité des équations algébriques dans un programme ambitieux. Il fait l'observation de deux phénomènes qui seront le point de départ de la dernière ligne droite d'un parcours long de 4 siècles
 

3.    Ruffini, Abel et Galois.

    Lagrange observe que les radicaux cubiques des formules de Scipion del Ferro peuvent se mettre sous la forme [ x[1] + w x[2] + w^2 x[3] ] / 3 où w est une racine cubique de l'unité et constate par ailleurs que le cube de cette expression ne prend que deux valeurs quelque soit la permutation des x[i], il remarque un phénomène analogue concernant l'équation du quatrième degré avec l'expression x[1] x[2] + x[3] x[4] . Il saisit l'importance de ses découvertes et déclare qu'elles constituent la métaphysique de la résolution du troisième et quatrième degré.

    Lagrange fait une autre découverte capitale en montrant que si V et V' sont deux expressions des rationnelles des racines invariantes sous les mêmes permutations alors l'une s'exprime comme une fonction rationnelle de l'autre, un résultat dont il souligne l'importance en déclarant :

    Ce problème me paraît un des plus importants de la théorie des équations, et la solution générale que nous allons en donner servira à jeter un nouveau jour sur cette partie de l'algèbre.

Avec ses résolvantes,  prélude aux célèbres sommes de Gauss, Lagrange introduit en 1770 les groupes de permutations dans la résolution des équations algébriques. II montre que la connaissance des n résolvantes :

obtenues en faisant varier z[i] dans l'ensemble des racines n-ièmes de l'unité entraine la connaissance des x[s]. Il montre que si n est premier alors les y[i]^n sont des racines d'une équation de degré n-1 dont les coefficients sont des fonctions rationnelles de racines d'une équation de degré (n-2)! des coefficients de l'équation de départ. Des travaux qui le conduisent à déclarer :

    Voilà si je ne me trompe, les vrais principes de la résolution des équations algébriques, et l'analyse la plus propre à y conduire; tout se réduit, comme on le voit, à une espèce de calcul des combinaisons, par lequel on trouve a priori les résultats auxquels on doit s'attendre.

  Alexandre Vandermonde poursuit les travaux de Lagrange et conjecture que les puissances (n-1)/2 ième des résolvantes de Lagrange sont des nombres rationnels. La preuve de cette assertion apparaît en bonne place dans les recherches arithmétiques de Gauss. Il affirme en déduire qu'un polygone régulier à n cotés est constructible à la règle et au compas si et seulement si n est un produit de nombres premiers de Fermat. Il s'agit là d'un énoncé typiquement Galoisien bien avant l'heure.

    Les méthodes de résolution par radicaux des équations de degré deux, trois ou quatre sont connues depuis le moyen âge et le dix-septième siècle.  Les algébristes  ne doutent pas de l'existence d'une méthode de résolution de l'équation du cinquième degré.  Paolo Rufini est le premier  a ne pas y croire et s'attaque à montrer l'impossibité de résoudre par radicaux l'équation générale du cinquième degré. Il propose une démonstration prolixe, obscure qui reste incomplète malgré de nombreuses tentatives d'amélioration. Les algébristes  de l'époque sceptiques ne peuvent pas etre convaincus par cette démonstration,  à l'exception d'Augustin Cauchy qui, et ce n'est pas dans ses habitudes, adresse  ses félicitations à  Ruffini.   La démonstration utilise les bons ingrédients : notions de substitutions et  théorie des groupes.

     Cette théorie des groupes qui germe dans les mémoires de Ruffini,  approfondie par Cauchy,  ne suffit pas pour démontrer correctement ce que j'appelle l'obstruction de Ruffini. Pour y parvenir, il faut inventer et développer un nouvel ingrédient : la théorie des corps. Abel est le premier à s'aventurer dans cette voie. Adolescent, il avait cru trouver une résolution par radicaux du cinquième degré. Il se rend compte de son erreur et n'a de cesse de prouver le contraire. Après plusieurs années d'efforts, il démontre sans faille le théorème de Ruffini.

     Abel décide de s'attaquer au problème général. Il s'agit d'établir un critère de solvabilité par radicaux d'une équation algébrique arbitraire. Il semble être proche du but quand la mort le terrasse en 1829. Trois ans plus tard, Galois entre en scène pour couronner l'édifice. La correspondance de Galois permet de relier avec une clarté étonnante chaque résolvante intermédiaire avec un sous-groupe du groupe de Galois. Une équation est résoluble par radicaux si et seulement si son groupe de Galois est résoluble.

    En particulier, une équation de degré cinq avec trois racines réelles et deux imaginaires ne peut-être résolue par radicaux parce que son groupe de Galois est isomorphe au groupe des permutations de cinq lettres qui n'est pas résoluble. En conclusion,  la théorie de Galois  prouve  avec une élégance remarquable l'impossibilité de résoudre l'équation générale de degré 5 et plus par radicaux, la raison essentielle est un argument de la théorie des groupes finis : la simplicité du groupe alterné.
 
 

4. Galoiseries

Trois ans après la disparition d'Abel, Galois donne la solution définitive. Il décrit précisément le contexte des équations algébriques : groupes et corps. Il définit les notions de corps de base, d'adjonction de racines et d'irréductibilité par rapport à un corps. Tout cela sans disposer du mot corps qui n'est introduit qu'à la fin du XIX par Dedekind. Galois parle de l'ensemble des nombres qui s'exprime rationnellement à partir des coefficients du polynôme sans utiliser la structure algébrique de ce dernier.

A une équation P(T) = 0, sans racine multiple dans un corps k, il montre :

On peut toujours former une fonction V des racines telle qu'aucune des valeurs que l'on obtient en permutant dans cette fonction les racines de toutes les manières ne soit égale à une autre

et que cette fonction

jouira de la propriété que toutes les racines de l'équation proposée s'exprimeront rationnellement en fonction de V

et que, V, V', V'', étant les autres racines de l'équation irréductible à laquelleV satisfait.

Si a = f(V) est une racine de la proposée, f(V') sera également une racine de la proposée.

Galois définit ensuite le groupe G de l'équation P sur k comme l'ensemble des permutations des racines xi qu'on obtient en substituant à V dans l'expression rationnelle de xi une quelconque de ses conjuguées V'. Il obtient la propriété caractéristique fondamentale de k : invariance par conjugaison. Ensuite, il montre que si K est un corps intermédiaire correspondant à un autre polynôme alors le groupe de ce dernier est un sous-groupe distingué de G, notion qu'il invente pour la circonstance. Après quoi, il peut donner son critère de résolubilité par radicaux. Une équation P(T) = 0 est résoluble par radicaux si et seulement s'il existe une chaîne de groupes

de sorte que chaque G[i] soit un sous-groupe distingué de G[i+1] et que chaque quotient G[i+1]/G[i] soit cyclique.

     Galois  soumet un mémoire  sur cette question à l'Académie des sciences dont les illustres représentants Fourier, Poisson  et Laplace... tous célèbres pour leurs travaux en analyse ne sont pas sensibles aux résultats du jeune algèbriste. Le document sera  purement et simplement perdu ! D'où la lettre ci-dessous adressé par Galois à Poisson. Cauchy suggère à Galois de présenter un second exemplaire de son mémoire qui est examiné par Poisson en personne.  Réglements de comptes ?  Embrouilles politiques ?  incompétence de Poisson ? Toujours est-il que le mémoire est jugé insuffisant.
 

5.    Les corps de Galois

    Les équations algébriques conduisent Galois vers les groupes. Inversement, les groupes conduisent Galois vers des corps que Dedekind appelle les imaginaires de Galois. Il s'agit des corps finis que les anglophones appellent les champs de Galois. Pour Evariste Galois les calculs modulo une congruence sont analogues à ceux qu'on peut faire dans le corps des nombres rationnels. Il n'hésite pas à adjoindre à ces corps des racines idéales pour construire de nouveaux corps finis qu'il utilise pour faire de l'algèbre linéaire des corps finis et obtenir ainsi de nouveaux goupes abstraits.

     La théorie de Galois est d'une rare richesse et magnifie tout ce qu'elle rencontre. Les arithméticiens purs font collaborer la théorie et les corps de Galois avec la théorie de la ramification pour obtenir des résultats profonds : loi de réciprocité, symbole d'Artin et théorie du corps de classe de Hilbert.

    Les arithméticiens appliqués (il en existe) traduisent les problèmes concrets dans le langage de Galois pour faire parler l'automorphisme de Frobenius dans le cadre des transmissions numériques. PathFinder utilise des corps de Galois pour envoyer ses images de la planète Mars, la transmission perturbée par tout ce qui traine dans l'espace est protégée par un code de Reed-Solomon qui est construit à partir des imaginaires de Galois. Le même principe permet de faire de la musique numérique sans craquement ni parasite à partir des disques compacts. Les corps de Galois permettent de construire les séquences utilisées dans les protocoles de partage de canal comme dans le téléphone cellulaire. Les radars discrets émettent des signaux très spéciaux dits à faible corrélation dont l'existence et la construction reposent à la fois sur la théorie de Galois et les corps finis et idem pour les fonctions booléennes hautement non-linéaires utilisées en cryptographie. Enfin, mais beaucoup moins sérieusement, j'ai eu l'occasion de gagner quelques dizaines de milliers de francs en jouant des configurations particulières dont la caractéristique est d'être stables sous l'action de certains sous-groupes linéaires  scalairisés sur un corps finis..

 6.    La théorie de Galois en quelques mots

    On constate que les sous-corps de C sont des Q-espaces vectoriels. Par définition, les  corps de dimension finie sont des corps de nombres. Ils correspondent aux extensions algébriques  de dimension finie sur Q.  Si x désigne  un élément d'un corps de nombre K alors le degré de x divise [K:Q] la dimension de K sur Q.

    Les sous-corps d'un corps de nombres K sont des corps de nombres. Si k désigne l'un d'entre-eux alors on dit que  K est une extension algébrique de k, c'est donc un k-espace vectoriel de dimension finie, le théorème des bases télescopiques montre que  [K : Q ] = [K : k] [ k : Q].

Les expressions rationnelles formées à partir des éléments deux extensions  algébriques K et Ld'un même corps de base kforment une extension algébrique, c'est le compositum deL et de K,  on le note KL. Lorsque l'intersection de K et L se réduit à k, les extensions sont dites linéairement disjointes.

Théorème de l'élément primitif.    Soit K/k une extension de corps de nombres. Il existe un élément x tel que K = k[x] c'est à dire que K est l'ensemble des expressions polynomiales en x à coefficients dans k. Dans ce cas, on dit que x est un élément primitif de K sur k.

   C'est un résultat d'algèbre linéaire qui simplifie l'exposé de la théorie de Galois. Partons d'une extension de corps de nombres K/k. Il existe un élément primitif x tel que K = k[ x ]. Si y est un conjugué de x alors le corps k[y] est isomorphe à K.  Ainsi, il  existe exactement [K : k]  homomorphismes de K dans C qui  fixent tous les éléments du corps de base.. L'objet de la théorie de Galois est l'étude des extensions au travers de ces homomorphismes. Les k-homomorphismes qui ont pour image K sont des k-automorphismes, il forme un groupe : le groupe de Galois de l'extension K/k. L'idée géniale de Galois consiste à traduire les propriétés algébriques en termes de groupes.
 

    Le groupe de Galois de K/k, noté gal(K/k), agit surK. Moralement le théorème de l'élément primitif montre que Gal(K/k)  n'est rien d'autre qu'un certain sous-groupe du groupe des permutations de symboles n=[K: k] : les  racines du polynôme minimal d'un élément primitif. Clairement l'ordre de  gal(K/k) est au plus n, c'est  exactement n lorsque K contient tous les conjugués d'un élément primitif K/k. Dans ce cas, on dit que l'extension K/k est galoisienne.  Il convient de remarquer sur le champ que si L/k est galoisienne alors  pour tout corps intermédiaire K, l'extension L/K est toujours galoisienne alors que K/k ne l'est pas forcément. Un des objectifs majeurs de la théorie de Galois est de clarifier cette question.  Par définition, une extension abélienne est une extension galoisienne à groupe de Galois commutatif. On définit de même les extensions cycliques.

    Soit A(X) un polynôme irréductible à coefficients dans k.  Notons L corps de décomposition de A, c'est le plus petit corps dans lequel A(X) se factorise en produit de facteur de degré un. L'extesnsion L/k est galoisienne, son degré est  inférieur ou égal à n! = 1x2x...xn. puisque ce dernier est complètement déterminé par son action sur les n racines de A. Par définition, le groupe de Galois de L/k s'appelle le groupe de Galois du polynôme A. Moralement, c'est un certain sous-groupe de S(n) le groupe des permutations de n lettres.

     L'idée fondamentale de la théorie de Galois est de faire le lien entre corps intermédiaires et sous-groupe du groupe de Galois gal(L/Q), afin  de déterminer les extensions Galoisiennes intermédiaires.  La correspondance de Galois associe à chaque corps intermédiaire K le sous-groupe g(K) formé des automorphismes de L qui laissent K invariants, et à chaque sous-groupe H de G, elle associe un sous-corps k(H) formé des éléments invariants par tous les éléments de H. Les applications g et k sont des applications décroissantes.

Théorème 1. Soit L une extension Galoisienne de Q. L'application k est une bijection de l'ensemble des sous-groupes de gal(L/Q) sur l'ensemble des corps intermédiaires, elle est inversible d'inverse g.
 

Théorème 2. Soit L une extension algébrique  de Q. Le corps des éléments fixés par le groupe de Galois de L/Q définit une extension intermédiaire K, et  L/K est galoisienne.

    L'extension  K/Q ne l'est pas toujours. Rappelons qu'un sous-groupe H est dit distingué (ou invariant ou normal) dans G lorsqu'il est invariant par automorphisme intérieur i.e. sH = Hs quel que soit s dans G.

Théorème 3. Soit L une extension Galoisienne de Q. L'application k est une bijection de l'ensemble des sous-groupes distingués de gal(L/Q) vers l'ensemble des corps intermédiaires qui sont des extensions galoisiennes de Q. Dans ce cas, le groupe de Galois gal(K/Q) est isomorphe au groupe quotient gal(L/Q) / H.
 

    Quand une puissance d'un élément y est dans un corps K, on dit que y est un radical de K. L'équation algébrique  A(X) = 0 est dite résoluble par radicaux s'il existe une suite finie y[1],  y[2],..., y[m] d'éléments algébriques tels que pour tout i<m, y[i+1] soit un radical du corps K[i] engendré par y[1], y[2], ..., y[i].

    Un groupe G est résoluble s'il existe une chaine de sous-groupes G[0]={1}, G[1], ..., G[m]=G tels que chaque G[i] est invariant dans G[i+1] avec un quotient abélien  G[i+1]/G[i].  Quand il en est ainsi, on peut raffiner la chaîne de sous-groupe pour faire apparaître des quotients cycliques.

Théorème 4.   Soient L et  K deux extensions algébriques finies d'un corps k. On suppose que L/k est galoisienne et on note LK le compositum de L et K. L'extension LK/K est galoisienne et la restriction à K des automorphismes de  LK/ K définit un isomorphisme sur  gal(L/k).
 

Théorème 5. L'équation A(X)=0 est résoluble par radicaux si et seulement si le groupe de Galois du corps de décomposition de A est résoluble.

Pour démontrer l'impossibilité de résoudre une équation par radicaux il suffit de trouver un polynôme ayant un groupe de Galois non résoluble !
 
 

7.    Obstruction du cinquième degré

    On sait que S(5) est engendré par le cycle de longueur 5 et une transposition. Considérons alors un polynôme de degré 5 admettant trois racines réelles et deux racines imaginaires comme par exemple X^5 -4X +2. Son groupe de Galois qui contient forcément un élément d'ordre 5, et un élément d'ordre 2 (la conjugaison usuelle) est isomorphe à S(5).

Simplicité de A(5):
Le groupe A(5) contient 60 éléments qu'on peut partitionner en quatre paquets : 1 élément unité,   15 involutions avec un point fixe,  20 tricycles, et 24 cycles de longueurs 5. Ces quatres paquets sont stables par conjugaisons. C'est clair pour les trois premiers, pour le dernier on peut utiliser un argument sur les sous-groupes de Sylow. Les nombres 15 + 1, 20 +1, et 24 + 1 qui ne sont pas des diviseurs de 60, ne peuvent pas être des ordres de sous-groupes de A(5).  La simplicité en découle.

Arguments de Sylow.
Soit p un nombre premier et soit G un groupe de cardinal p^rq, avec p ne divisant pas q. Par définition, un p-groupe de Sylow de G est un sous-groupe maximal d'ordre égal à une puissance de p. Les théorèmes de Sylow affirment que les p-sous-groupes de Sylow  de G sont deux à deux conjugués, d'ordre égal à p^r et leur nombre congru à 1 mod p divise q.
 

8.    Le second degré à la Galois.

Supposons que P(X) = aX²- bX + c soit irréductible sur Q et notons x et y ses deux racines qui satisfont aux égalités :

Le groupe de Galois du polynôme est réduit à deux éléments : l'identité et une transposition T qui échange x et y. Nous devons trouver un radicalrnécessairement de degré deux, solution d'une équation de la former² + d = 0, avec d rationnel. Il s'agit donc de trouver une un élément rde Q(x,y)tel que r² soit dans Q mais pasr.

Je vous laisse chercher un peu? Ca y est ? Bien, vous avez sans doute réalisé que r = x - y convient. En effet, T(r) = -r et donc rn'est pas rationnel puisqu'il n'est pas fixé par le groupe de Galois contrairement r² en  qui est un rationnel dqu'il nous reste à déterminer par les relations entre racines et coefficients.

et à partir de là, vous retrouvez xet y en fonction de a, b, c et d.

Pouquoi faire compliqué quand on peut faire simple ?

Ce qui suit devrait nous éclairer.
 

9.     Le troisième degré à la Galois.

 Le lecteur est chaud pour appliquer Galois, alors laissons temporairement cette méthode de côté. Un changement de variable affine, permet de se ramener à une  équation de la forme :

 Nous supposons P irréductible, ce qui est équivalent à dire que ses trois racines x, yet z ne sont pas rationnelles. Elles satisfont aux égalités :

 
 x + y + z = 0
xy + yz + xz = p
xyz = q

 Supposons que ce soit S(3). Notons S la permutation circulaire S(x) = y, S(y) = z et S(z) = x. Trichons un peu ( le théorème 4 nous y autorise) et faisons comme si le corps des nombres rationnels contenait j, l'une des deux racines troisièmes primitives l'autre étant j². Notez qu'en réalité j est de degré deux, car  j³ = 1et donc 1 + j + j² = 0. Comme précédemment, nous utilisons la résolvante de Lagrange

Remarquez alors que le cube de r est invariant par S  car  j³ = 1. La théorie de Galois prévoit que r³ est un nombre quadratique D que nous déterminerons quelques lignes plus bas.  En fait r est une racine cubique parfaite puisque ses conjugués sont j²r et jr.

Calculons D  :

La quantité w :=   6 x y z + x³ + y³  + z³ est rationnelle, et les quantités u:= x² y + x z²  + y² z  et v:=  x² z + x y²  - 3 y z²sont conjuguées par les transpositions de  S(3). Ce qui précède suffit pour comprendre les raisons profondes qui font que l'équation du troisième degré est résoluble par radicaux. Pour aller plus loin, nous devons déterminer l'équation du second degré qui annulle u et v. Il faut un peu de courage pour exprimer leurs somme et produit en terme des fonctions symétriques des racines x,  y, et z. Le cas de la somme est immédiat :

Pour le produit, c'est un peu plus délicat. Les relations suivantes ( relations de Newton ) sont précieuses :

          x²+y²+z²  = ( x+y+z)² - 2 (xy+yz+zx) = -2p
          x³+y³+z³  =  (x+y+z)³ - 3 (xy+yz+zx)(x+y+z) + 3xyz = 3q

d'où l'on tire :

En jouant avec les relations de Newton, on obtient  x³y³ + y³z³ +z³x³ = p³+3q² et le discriminant pointe son nez !

X.    Troisième degré : la méthode de Tartaglia

Le plus souvent (mais toujours à tort) dite méthode de Cardan. Nous partons de l'équation:

 Les realtions entre coefficients et racines x, y et z s'écrivent : x + y + z = 0,  xy + yz + xz = 3p et xyz = q. L'astuce remarquable de Tartaglia consiste à substituer x par u + v. Nous obtenons une équation de deux variables

Une condition suffisante pour obtenir une racines réside dans le système   u³ +   v³ = q et uv = p qui fait apparaître somme et produit des racines d'une équation du second degré par un dernier changement de variable U =  u³ et V =  v³

D'où l'on tire U = (q + Racine[q² + 4p] ) / 2 et V = (q - Racine[q²+ 4p] ) / 2. Il ne reste plus à extraire des racines cubiques et reoller les bons morceaux. Si u+vest une des racines alors les autres sontu+j v et u+ j² v.
 
 

B.     Le quatrième degré à la Galois

A laquelle est associée une chaine de corps :

Ainsi l'équation générale de degré 4 est résoluble par radicaux. De plus,  comme l'extension M/N est cubique, et
que les trois autres N/Q, L/M et K/L sont quadratiques, nous en déduisons  que la formule minimale de résolution doit être composée d'un radical cubique et deux  trois extraction de racine carrée. Nous venons donc de deviner la formule de résolution d'une équation assez complexe sans faire le moindre calcul. Aucun doute, nous sommes bien entrain de faire de l'algèbre !

C.     Quatrième degré : la méthode de Ferrari

D.    Quelques liens supplémentaires :

• histoire des maths.
• The life of Galois
• Evariste Galois
• Images de mathématiciens
• la vie de Galois
• Biographies de mathématiciens
• Présence d'Evariste Galois, A.P.M.E.P numéro 48, année 1982.
• Cours d'algèbre, Daniel Perrin.
• Chapitre VI      Algebra   de  Serge Lang
• Chapitre IV     Algèbre    du groupe Nicolas  Bourbaki