Euclide :

le septième élément.

1.  Quelques aspects historiques

2.  Une curiosité

3. L'algorithme d'Euclide

4. Liens et références

1.  Quelques aspects historiques


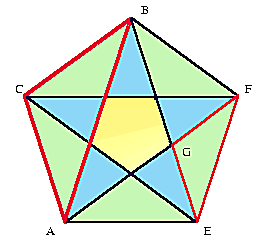
Le pentagone est le symbole des pythagoriciens. Il illustre les connaissances géométriques et arithmétiques de la Gréce antique. On le construit à la règle et au compas en utilisant le théorème de Pythagore. On observe des médiatrices, des relations d'orthogonalité, des parallèles... Une fois repéré un losange, le théorème de Thalès montre la similitude des triangles ABC et EFG. En son centre brille le nombre Phidias rapport de la dite similitude qui se trouve être le rapport d'un diamètre sur côté ! La figure se reproduit à l'infini et suggère à Hépitarque l'incommensurabilité de la divine proportion plus connue comme le nombre d'or.

Par tradition, l'école pytagoricienne ne laisse aucun écrit. Le savoir grec sera en partie préservé par l'oeuvre encyclopédique d'Euclide d'Alexandrie. Une oeuvre composée de 13 livres : les éléments. La majorité du texte est consacrée à la géométrie, le reste porte sur les nombres et les questions d'irrationalité. Les éléments qui concernent la géométrie et s'appliquent à l'architecture et à la construction des cathédrales traversent les siècles sans difficulté!

    Les questions arithmétiques sont exposées dans les éléments sept et neuf. Le septième élément  traite des nombres et des mesures de grandeurs, de la division euclidienne et de l'algorithme d'Euclide. Dans le neuvième élément, Euclide  démontre que l'ensemble des nombres premiers  est infini,  un livre qui contient la définition des nombres parfaits et une proposition les concernant à savoir : si   1 + 2 + ... + 2^s est un nombre premier S  alors  S 2^(s-1) est un nombre parfait...

    La légende raconte que ces textes sont restés oubliés pendant plusieurs siècles, à cause  du manque d'intérêt des hommes envers l'arithmétique, et même, qu'ils auraient failli disparaître à cause des guerres et des incendies. J'ai photocopié quelques pages d'une version latine du Livre vii des éléments d'Euclide à partir d'un ouvrage du xvii-ième siècle que vous pouvez consulter à la bibliothèque du CIRM. Dans les deux premières pages, Euclide énonce ses 12 postulats sur les nombres. L'algorithme d'Euclide et la division Euclidienne sont dans la dernière page.
 

page 314 page 315 page 316

    Jusqu'au milieu du XX-ième siècle, l'arithmétique est considérée comme une science pure, fondamentale. La discipline reine des mathématiques. Le mathématicien Hardy déclare :

 
... both Gauss and lesser mathematicians may be justified in rejoicing that there is one science (number theory) at any rate, and that their own, whose remoteness from ordinary human activities should keep it gentle and clean...
A mathematician'Apology, 1940.
    Les choses ont bien changé ces dernières années et les algorithmes tel que celui du calcul du PGCD de deux entiers sont au coeur de l'actualité pour leurs applications cryptographiques. Le cryptosystème RSA s'appuie sur la difficulté (admise) de factoriser un entier de plusieurs centaines de chiffres. L'algorithme d'Euclide donne lieu à des généralisations : algorithme de Gauss et LLL qui ont pour objet la recherche de vecteurs courts dans les réseaux et qui sont utilisés pour casser certains cryptosystèmes

2.  Une curiosité

Le pentagone est le siège d'une troublante relation entre le nombre de la bête DCLXVI et la divine proportion. Notons w la racine principale cinquième de l'unité. De la relation w^5 - 1 = 0 et donc
1 + w + w^2 + w^3 + w^4 = 0.
Nous tirons que
x := * cos( 3 * 2pi/5 ) = w^3 + w^2
est solution de l'équation :
x^2 + x - 1 = (w^3 + w^2)^2 + (w^3+w^2) = w + 2 + w^4 + w^3 + w^2 - 1 = 0
Le discriminant vaut 5, x est la racine réelle négative :
x = ( -1 - R( 5 ) ) / 2 = - phi
C'est l'opposé du nombre d'or, la divine proportion. Un dernier petit calcul montre que le rapport 216 / 360 se réduit à 3 / 5, au final, nous obenons l'étrange relation :
sin( 666° ) = cos ( 6*6*6° ) = - phi / 2
En effet, 666 - 6*6*6 = 90 modulo 360 !

3.  L'algorithme d'Euclide

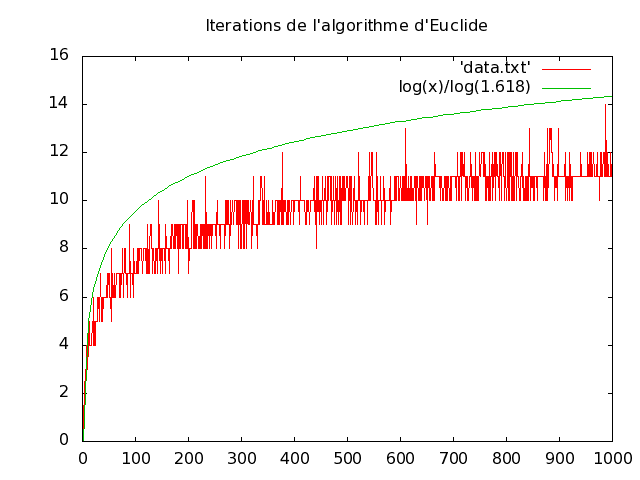
L'algorithme d'Euclide s'écrit en quelques lignes.  En voici une version récursive PGCD(x,y) qui comme son nom l'indique, retourne le pgcd de deux entiers x et y. La complexité de l'algorithme dépend du nombre d'appels récursifs  nécessaire au calcul de pgcd(x,y) . Au milieu du XIX-ième Gabriel Lamé utilise la suite de Fibonacci pour démontrer que le nombre d'itérations de l'algorithme d'Euclide est logarithmique en la plus grande des entrées. Le résultat est optimal comme le précise par la suite Edouard Lucas. 

PGCD( x, y  : nombre )
SI y > 0 RETOURNER PGCD( y, x mod y )
SINON RETOURNER x
FSI 

EUCLIDE( x, y  : nombre )
TANTQUE ( Y > 0 )
      x, y := y , x mod y
FTQ
RETOURNER x
FSI
Une petite modification de l'algorithme d'Euclide permet de résoudre l'identité de Bachet-Bézout dont la version itérative la plus efficace est celle de Blankenship. 
BACHET( x, y  : nombre )
X := ( 1, 0, x )
Y := ( 0, 1, y )
TANTQUE ( Y[3] > 0 )
      q    := X[3] div Y[3]
      X, Y :=  Y,  X - q * Y
FTQ
RETOURNER x
FSI

Exercice 1.    Sept divisions euclidiennes sont nécessaire à l'algorithme d'Euclide pour certifier premiers entre-eux les nombres (x,y).    Quels sont ces nombres ?

Exercice 2.    Soit F[n] le n-ième nombre de Fibonacci. F[0]= F[1] = 1 et F[n+1] = F[n] + F[n-1]. Vérifier que

PGCD( F[n], F[m] ) = F[ PGCD(m,n) ] !

Exercice 3.    Ecrire un algorithme récursif pour calculer deux  entiers u et v tels que

xu+yv = PGCD(x,y)

4. Liens et références

  1. H. D., Ebbinghaus et autres, Les nombres, Vuibert 1998.
  2. G. Kayas, Euclide les éléments. Edition du CNRS, 1978.
  3. P. Langevin, une brève histoire des nombres.
  4. R. Seroul, math-info : informatique pour mathématicien, InterEdition 1995.
  5. D.  Lancon, An Introduction to the Works of Euclid With an Emphasis on the Elements
[home page ]   [Euclide ]   [Gauss ]   [Galois ]   [Paley ]   [Fermat ]   [Lasker ]   [Fourier ]   [Riemann ]   [RSA ]
 Philippe Langevin, décembre 1999, février 2000, décembre 2013.